本文目录一览:
1、求根公式是什么2、数学求根公式是什么?3、求根公式是什么?4、求根公式是什么?5、根的公式是什么呢?6、求根公式怎么写请给写一下求根公式是什么
求根公式如下:
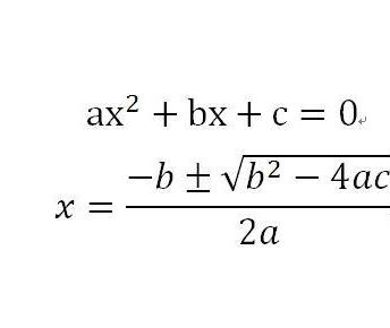
a为二次项系数,b为一次项系数,c是常数。
一元二次ax^2 +bx+c=0可用求根公式x= 求解,它是由方程系数直接把根表示出来的公式。这个公式早在公元9世纪由中亚细亚的阿尔·花拉子模给出。
用求根公式法解一元二次方程的一般步骤为:
①把方程化成一般形式 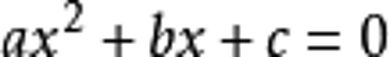
,侍盯确定 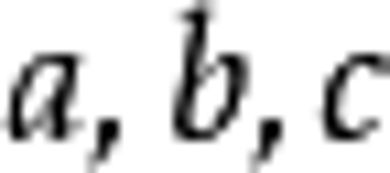
的值(注意符号);
②求出判别式 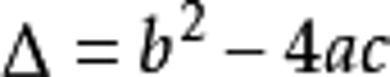
的值,判断根的情况;
③在 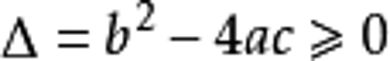
(注:此处△读“德尔塔”)的前提下,把 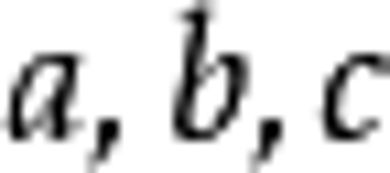
的值代入公式 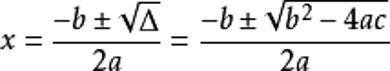
进行计算,求出方程的根。
一元二次方程成立必须同时满足三个条件:
①是整式方程,即等号两边都是整式,桥核方程中如果有分母;且未知数在分母上,那么这个方程就是分式方程,不是一元二次方程,方程中如果有根号,且未知数在根号内,那么这个方程也不是一元二次方程(是无理方程)。
②只含有一个未知数;
③未知数项的最高次数是2。
数学求根公式是什么?
求根公式如下:
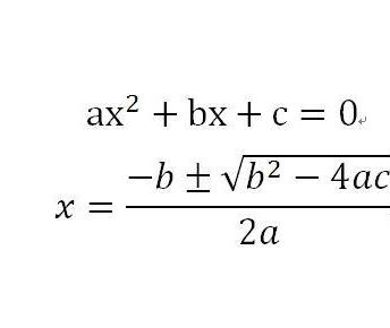
a为二次项系数,b为一次项系数,c是常数。
一元二次ax^2 +bx+c=0可用求根公式x= 求解,它是由方程系数直接把根表示出来的棚数晌公式。这个公式早在公元9世纪由中亚细亚的阿尔·花拉子模给出。
求根公式是什么?
求根公式为:
ax²+bx+c=0,a≠0
x1=[-b-√(b²-4ac)]/(2a)
x2=[-b+√(b²-4ac)]/(2a)
韦达定理为:
x1+x2=-b/a
x1*x2=c/a
发展历史:
法国数隐戚学家弗朗索瓦·韦达在著作《论方程的识别与订正》中改进了三、四次方程的解法,还对n=2、3的情形,建立了方程根与系数之间的关系,现代称之为韦达定理。
韦达最早发现代数方程的根与系数之间有这种关系,档携键因此,人们把这行巧个关系称为韦达定理。韦达在16世纪就得出这个定理,证明这个定理要依靠代数基本定理,而代数基本定理却是在1799年才由高斯作出第一个实质性的论性。
求根公式是什么?
通用求根公式是x=[-b±根号(4ac-b平方)隐念]/2a
一般过程:
原式为ax�0�5+bx+c=0
当b�0�灶纯困5-4ac>=0时有两个根
x1=(-b+√(b�0�5-4ac))/2a
x2=(-b-√(b�0�5-4ac))/2a
当b�0�5-4ac<0时
x1=x2=-b/裤友2a
根的公式是什么呢?
根公式是由方程系数直接把根表示出来的数学计算公式。
标准式:ax²+bx+c=0(a≠0)。
求根公式:x=[-b±√(b²-4ac)]/2a。
一元二次ax^2 +bx+c=0可用求根公式x= 求解,它是由方程系数直接把根表示出来的公式。这个公式早在公元9世纪由中亚细亚的阿尔·花拉子模给出。

有清并关公式:
至于一元四次方程ax^4+bx^3+cx^2+dx+e=0求根公式由卡当的学生弗拉利找到了。
关于三次、四次方程的求根公式,因答蔽迹为要涉及复数概念,这里不介绍了。
一元三次、四次方程并虚求根公式找到后,人们在努力寻找一元五次方程求根公式,三百年过去了,但没有人成功,这些经过尝试而没有得到结果的人当中,不乏有大数学家。
后来年轻的挪威数学家阿贝尔于1824年所证实,n次方程(n≥5)没有公式解。不过,对这个问题的研究,其实并没结束,因为人们发现有些n次方程(n≥5)可有求根公式。
求根公式怎么写请给写一下
一元二次方程丛歼ax^2+bx+c=0(a≠0)的求根公式为乱郑迟:x=[-b±√(b^2-4ac)]/2a(b^2-4ac≥0).
推导过程如下:ax^2+bx+c=0(a≠0)的两边都除以a得,
x^2+b/ax+c/a=0,哗李x^2+b/ax+(b/2a)^2=(b/2a)^2-c/a,(x+b/2a)^2=(b^2-4ac)/4a^2.
(1)当b^2-4ac<0时,原方程无实数根.
(2)当b^2-4ac≥0时,原方程的解为x=[-b±√(b^2-4ac)]/2a,