高中数学(高中数学有哪些)

高中数学是一门非常重要的学科，它涵盖了代数、几何、三角函数、微积分等多个方面。

高中数学的主要内容如下：

1.代数

代数部分包括整数、有理数、实数、复数等内容。在这个部分，学生将学习如何进行代数运算，如加、减、乘、除等，以及如何使用括号来简化代数式的表示。代数的研究对象不仅是数字，而是各种抽象化的结构。

2.几何

几何部分包括平面几何和立体几何。在这个部分，学生将学习如何通过画图和度量来解决几何问题。他们将学习三角形、四边形、圆等基本几何形状的性质和计算，以及如何应用这些知识来解决实际问题。

几何是研究空间结构及性质的一门学科。它是数学中最基本的研究内容之一，与分析、代数等等具有同样重要的地位，并且关系极为密切。

3.三角函数

三角函数部分包括三角函数的定义和性质，如正弦、余弦、正切等。在这个部分，学生将学习如何使用三角函数来解决各种问题，如计算角度、距离、面积等。

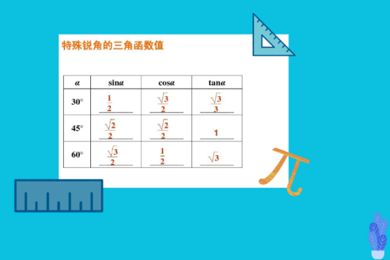
三角函数是基本初等函数之一，是以角度（数学上最常用弧度制，下同）为自变量，角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。

4.微积分

微积分部分包括导数和微积分。在这个部分，学生将学习如何使用导数来计算函数的变化率，以及如何使用微积分来解决各种实际问题，如极值问题、速度和加速度的计算等。

5.其他

除了以上的主要内容外，高中数学还包括线性代数、概率论与统计学等内容。这些内容虽然不是高中数学的必修课程，但是对于理解高中数学的其他内容和应用数学知识解决实际问题都有很大的帮助。

高中数学主要知识点如下：

1、函数与方程

函数与方程是高中数学的基础，包括一元二次方程、一元二次函数、指数函数、对数函数、三角函数等等。学生需要掌握如何解方程、求函数的性质和图像等。

2、数列与数列极限

数列是由一定规律产生的数的排列，数列极限是数列中的数随着项数的增加逐渐接近某个确定值。学生需要了解数列的定义、性质以及数列极限的计算方法。

3、数与数量关系

数与数量关系是研究数与实际问题之间的对应关系，包括直线函数、平面向量、等差数列、等比数列等。学生需要学会利用数与数量关系解决实际问题。

4、几何与三角形

几何是研究空间形态和图形性质的学科，高中数学中主要包括平面几何和立体几何。三角形是平面几何中的基本图形，学生需要了解三角形的性质、相似三角形、三角函数等。

5、概率与统计

概率与统计是研究随机事件和数据分析的学科。概率是研究随机事件发生可能性的大小，统计是研究数据的收集、处理、分析和解释。学生需要掌握概率计算方法和统计分析技巧。

6、微积分

微积分是数学中的一个重要分支，研究函数的变化率与积分的反操作。高中数学中主要包括导数与微分、积分以及微分方程等内容。学生需要学会求导、求不定积分、解微分方程等。

通过学习这些内容，学生可以培养数学思维和问题解决能力，为将来的学习和职业发展打下坚实的基础。要想在高中数学中取得好成绩，学生需要提前规划学习时间，理解概念，掌握基本的计算方法，并通过大量的练习提升自己的解题能力。

高中数学内容涵盖了许多重要的数学概念和技巧，包括代数、几何、函数、微积分等，旨在培养学生的数学思维和解决问题的能力。

1.代数：

代数是高中数学的基础，它研究各种数学符号和运算规则。在代数中，学生将学习解方程、简化表达式、因式分解、二次函数等概念和方法。代数是分析和解决各种问题的重要工具，也为后续学习提供了坚实的基础。

2.几何：

几何是研究形状、大小、相对位置和空间关系的数学分支。在高中数学中，学生将学习几何的基本概念，如点、线、面，以及各种几何形状的性质和定理。几何不仅培养了学生的空间想象力，还培养了逻辑推理和证明的能力。

3.函数：

函数是数学中一个重要的概念，描述了一个变量与另一个变量之间的关系。在高中数学中，学生将学习函数的定义、性质和图像，包括线性函数、二次函数、指数函数、对数函数等。函数是数学建模和实际问题求解的关键工具。

4.微积分：

微积分是研究变化和运动的数学分支，包括微分和积分两个方面。在高中数学中，学生会初步接触微积分的概念和基本技巧，如导数、极限和定积分。微积分是理解自然界和许多实际问题的数学语言。

5.概率与统计：

概率与统计是研究随机现象和数据分析的数学分支。学生将学习概率的基本原理和方法，如事件概率、条件概率和期望值。统计则涉及数据收集、整理、分析和解释，包括图表的制作、数据的描述性统计和推断统计等。

6.解析几何：

解析几何结合了代数和几何的方法，研究了平面和空间的几何对象通过坐标表示和运算的问题。学生将学习直线、圆、曲线等几何对象的解析表示和性质，以及解析几何在问题求解中的应用。

总结：

高中数学内容包括代数、几何、函数、微积分、概率与统计等多个重要模块。通过学习这些内容，学生可以培养数学思维、逻辑推理和问题解决能力，并为未来的学习和职业发展奠定坚实的数学基础。数学作为一门抽象而精确的学科，不仅仅有学术价值，还广泛应用于科学、工程、经济、计算机科学等领域，对个人和社会的发展都具有重要影响。