球体的体积公式:V=(4/3)*π*R^3(V:表示球体的体积,R:表示球体的半径)。
球的体积公式证明:
欲证(4/3)*π*R^3,可证(1/2)V=(2/3)*π*R^3做一个半球h=r, 做一个圆柱h=r(如下图)
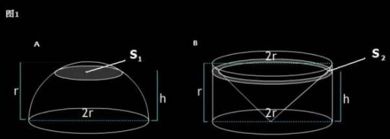
因为V柱-V锥= π×r^3- π×r^3/3=2/3π×r^3,所以若猜想成立,则V柱-V锥=V半球。
根据祖暅原理,夹在两个平行平面之间的两个立体图形,被平行于这两个平面的任意平面所截,如果所得的两个截面面积相等,那么,这两个立体图形的体积相等。若猜想成立,两个平面:S1(圆)=S2(环)。
1、从半球高h点截一个平面根据公式可知此面积为π×(r^2-h^2)^0.5^2=π×(r^2-h^2)
2、从圆柱做一个与其等底等高的圆锥:V锥 根据公式可知其右侧环形的面积为π×r^2-π×r×h/r=π×(r^2-h^2)。
所以π×(r^2-h^2)=π×(r^2-h^2),V柱-V锥=V半球,V柱-V锥=π×r^3-π×r^3/3=2/3π×r^3,所以V半球=2/3π×r^3。
由V半球可推出V球=2×V半球=4/3×πr^3,证毕,得出球的体积公式为V=(4/3)*π*R^3。